Как скажет вам любой эксперт по GRE, Quantitative section — это проверка на сообразительность, а не на умение считать. Ее также можно назвать психологическим тестом, созданным, чтобы напугать неопытного участника большими и страшными на вид числами.
К счастью, всегда есть метод укрощения математического безумства GRE и, следовательно, способ сделать эти пугающие числа более простыми для понимания. И именно здесь древо множителей — одно из наиболее сильных орудий в арсенале против математики в GRE — оказывается полезным.
Основы древа множителейВы можете с любовью (или без нее) вспомнить создание деревьев множителей в начальной школе. Они позволяют разбить крупное число на более мелкие и удобные части.
Для начала нам следует рассмотреть основы того, как найти простые множители. Мы начнем с использования заурядного древа множителей, плодом которого служит любое положительное сложное число.
К примеру, мы хотим найти простые множители 60.
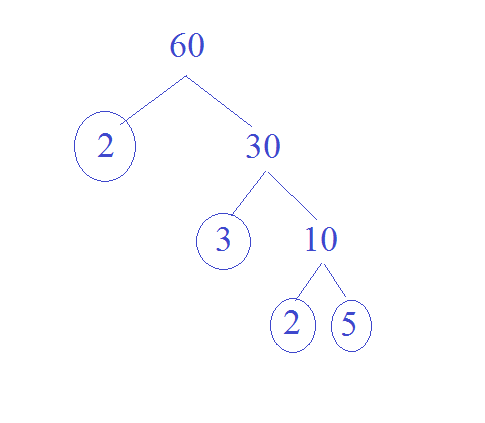
Мы можем начать с любых двух множителей 60, оба из которых будут меньше 60, а при перемножении дадут именно это число. Здесь мы берем 2 и 30. Каждый раз, находя простое число, обводим его, потому что эта «ветка» заканчивается. В данном примере 2 — простое, значит, заключаем его в круг.
Далее мы точно так же можем разбить 30: используем 3 и 10, обводим 3 — простое число. Затем мы делим 10 на 2 и 5, каждое из которых тоже простое, и помещаем их в кружочки.
Все это сообщает нам о числе 60 следующие вещи. Сразу же понятно, что его простыми множителями являются 2, 3 и 5. А что еще более важно, мы узнаем: 60 можно представить как произведение тех чисел, которые мы обвели совсем недавно: 2 х 2 х 3 х 5.
Запомните простые числаПростые числа — это кирпичики любого положительного сложного числа. Иначе говоря, любое положительное сложное число может быть представлено как множество простых чисел, перемноженных между собой.
Заучивание хотя бы нескольких первых простых чисел — 2, 3, 5, 7, 11, 13 — обязательно принесет пользу любому целеустремленному чемпиону GRE. Вы заметите, что 2 — это самое маленькое и единственное четное простое число. Запомните, не все нечетные числа после 2 простые (например, 9 — сложное число, потому что оно делится на 3), но после 2 все простые числа относятся к нечетным.
Укрощение математики GREИтак, чем полезна эта информация для решения Quantitative section? Деревья множителей — это просто нечто, сочиненное математиками для увеличения объема материала, который приходится изучать студентам перед GRE? Может, стоит обсудить это на вечеринках?
Напротив, нахождение простых множителей может сберечь ваше время и усилия при решении Quantitative section на экзамене GRE, если вы знаете, как применить эту концепцию. Каждый раз, когда вам кажется, что GRE пытается заставить вас перемножать или делить очень большие числа — давайте использовать научный термин «БСЧ» от Большие Страшные Числа — это прекрасный шанс на применение разложения на простые множители в качестве обходного пути.

Представьте, что GRE выдает вам следующую формулу и просит найти b:
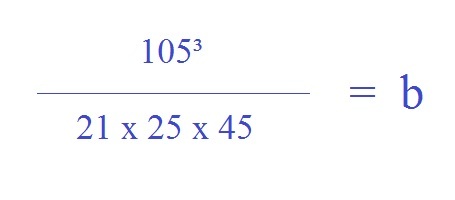
Может быть, математические боги GRE испытывают сострадание к бедным душам, которые собираются сидеть и искать, сколько же будет 105 х 105 х 105, а потом найти точное произведение 21 х 25 х 45 и в конце разделить одно БСЧ на другое. Как вам такой пример неэффективности?
Само критическое мышление приходит здесь на помощь [место для вставки любимой патетической музыки]. Студенты должны подумать: «GRE мог бы выдать мне любые числа в мире, поэтому должна быть какая-то причина, почему здесь выбраны именно эти». Подобная задача сама приводит к применению разложения на простые числа. А после этого математические действия становятся относительно безобидными.
Простые множители — ваши друзьяЧтобы решить предложенную выше задачу, давайте начнем со знаменателя. Используя деревья множителей, находим: 21 = 3 х 7, 25 = 5 х 5, а 45 = 3 х 3 х 5.
Теперь перейдем к числителю. В задаче сказано: 105³, поэтому давайте начнем со 105. Просто взглянув на 105, мы можем сказать, что оно кратно 5. Но 105 — это сколько раз по 5? Хорошо, 5 х 20 будет ровно 100, значит, нам нужна еще одна пятерка. Итак, 105 = 5 х 21, а 21 раскладывается на 3 х 7, как мы уже видели выше. Следовательно, 105 = 3 х 5 х 7. Однако у нас 105 в кубе. Поэтому мы должны трижды написать эту комбинацию в числителе.
Получаем:
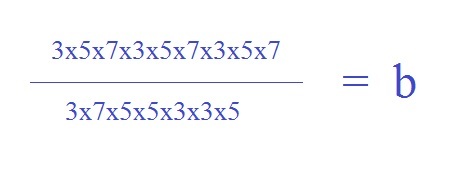
Это превращается в упражнение, которое математики называют — пользуясь еще более научной терминологией — «вычеркивание». Давайте применим тактику ниндзя для как можно большего количества чисел в верхней и нижней частях дроби и посмотрим, что останется. Вычеркиваем все тройки и пятерки и только по одной семерке сверху и снизу. Вуаля, в результате получаем просто 7 х 7, или 49.
Придется немного поупражняться в вербальной части, но математика уже не так пугает, верно? И да, не стесняйтесь, приносите деревья множителей на вечеринки... или не делайте этого, если хотите продолжать получать приглашения.
Автор перевода — Давиденко Вячеслав, основатель компании MBA Consult.